Bonjour et bienvenue sur Net Cours
Le tableau ci-dessous donne la répartition des salaires mensuels, en euros, des employés d’une entreprise :
- Calculer le salaire moyen dans cette entreprise. Que penser d’un tel résultat ?
- Dans cette entreprise, combien d’employés gagnent au plus 1050 euros ?
Dresser le polygone des effectifs cumulés croissants et lire une valeur approchée de la médiane et de Q1 et Q3 - Calculer de manière précise la médiane et les quartiles Q1 et Q3
- Construire le diagramme en boîte de la série statistique
Solution:
- Pour calculer le salaire moyen de l’entreprise, il faut considérer le milieu de chaque classe :
 Le salaire moyen dans cette entreprise est donc de 993 €. Il n’est pas forcément très représentatif de cette entreprise, car plus de la moitié des employés y gagnent plus de 1000 euros !
Le salaire moyen dans cette entreprise est donc de 993 €. Il n’est pas forcément très représentatif de cette entreprise, car plus de la moitié des employés y gagnent plus de 1000 euros !
2. Pour répondre à cette question, il faut dresser le tableau des effectifs cumulés croissants :
Ainsi, 165 employés gagnent au plus 1050 euros, au sein de cette entreprise
A partir de ce tableau, on dresse le polygone des effectifs cumulés croissants.
A partir de ce tableau, on dresse le polygone des effectifs cumulés croissants.
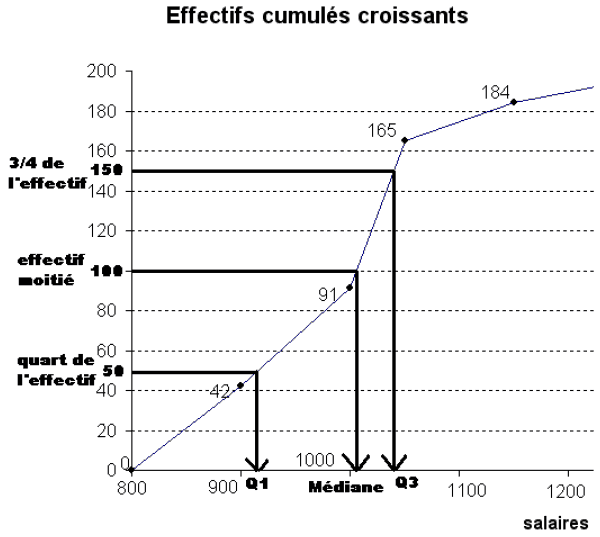
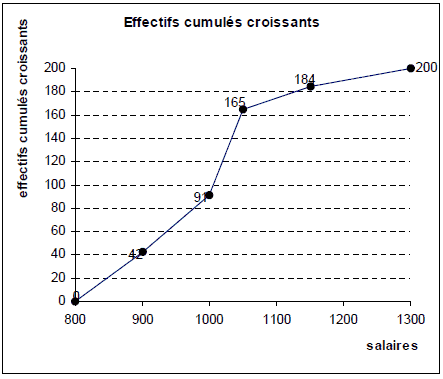 A partir de ce polygone, on cherche le salaire médian, c’est-à-dire celui qui va partager la série statistique en deux parties d’égale amplitude. Il s’agit donc du salaire correspondant à un effectif cumulé de 100 salariés (moitié de l’effectif). On se place ainsi que l’axe des ordonnées à l’effectif cumulé 100, et on lit l’antécédent de 100. Ce sera la médiane. On procède de même avec les quartiles Q1 et Q3, qui correspondent respectivement à un effectif cumulé de 1/4 x200 = 50 et de 3/4 x 200 = 150 On lit graphiquement que Médiane ≈ 1010 , Q1≈915 et Q3≈1050
A partir de ce polygone, on cherche le salaire médian, c’est-à-dire celui qui va partager la série statistique en deux parties d’égale amplitude. Il s’agit donc du salaire correspondant à un effectif cumulé de 100 salariés (moitié de l’effectif). On se place ainsi que l’axe des ordonnées à l’effectif cumulé 100, et on lit l’antécédent de 100. Ce sera la médiane. On procède de même avec les quartiles Q1 et Q3, qui correspondent respectivement à un effectif cumulé de 1/4 x200 = 50 et de 3/4 x 200 = 150 On lit graphiquement que Médiane ≈ 1010 , Q1≈915 et Q3≈1050
3) Calcul précis de la moyenne et des quartiles Q1 et Q3
Pour calculer la médiane, on va réaliser une interpolation linéaire entre les points A(1000 ;91) et B(1050 ;165)
L’équation de la droite (AB) est de la forme :
Pour trouver la valeur de p , on utilise les coordonnées de A (ouB !) :
 L’équation de (AB) est donc: 1,48x- 1389 . On trouve la médiane en calculant l’antécédent de la moitié de l’effectif (c’est à dire 200/2=100) par la fonction affine :
L’équation de (AB) est donc: 1,48x- 1389 . On trouve la médiane en calculant l’antécédent de la moitié de l’effectif (c’est à dire 200/2=100) par la fonction affine :
Ainsi Me≈1006
Puisque le quartile Q3 semble lui aussi appartenir à l’intervalle [1000;1050[, on utilise la même droite, et on résout l’équation 1,48x−1389=150 ⇔ 1539/1.48
≈ 1039,86
≈ 1039,86
Ainsi Q3≈1040
De la même manière, pour déterminer le quartiles Q1, on doit déterminer l’équation de la droite reliant les points (900 ;42) et (1000 ;91). Cette droite a pour équation v=0,49x−399, et la résolution de l’équation 0,49x-399=50 ⇔
x= 449/0.49 ≈ 916,33 fournit Q1≈916
x= 449/0.49 ≈ 916,33 fournit Q1≈916
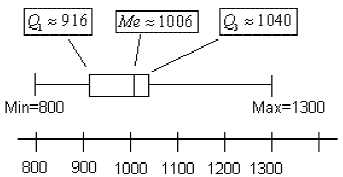
4.Le diagramme en boîte de la série est donné par :
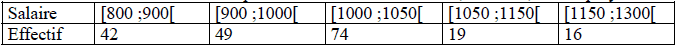
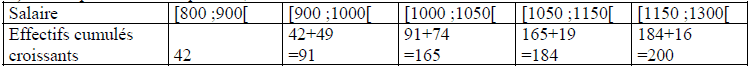
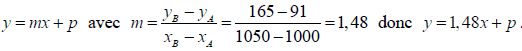

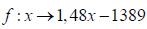

Aucun commentaire:
Enregistrer un commentaire